Depth-First Search
Depth-first search is a commonly used algorithm for traversing/searching a graph. This method starts with one of the vertices (let us call it, the source vertex). In this algorithm, we start from a source vertex and search the entire graph. When doing the search, we work on the vertex that has been discovered the most recently and then go to one of the neighbors of this vertex, and then go to the neighbor of this vertex of the earlier discovered vertex, and so on. This way, we keep exploring the graph in depth. Once we have reached a node such that all of its neighbors have already been visited (or are being visited), we backtrack to its parent, and then go to the next sibling node of the parent -- we keep backtracking until we reach the source vertex again. Depth-first search assumes that the nodes in the graph are connected. If they are not, then the algorithm traverses only those nodes that belong to the partition of the source node.
Let us now see how the depth-first search algorithm works in more detail. For that, we begin with a simple graph (provided below). The graph has 5 vertices and 5 edges. For the sake of simplicity, we keep the graph undirected.
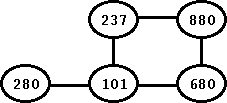
Figure: An Undirected Graph
For the above graph, we start with the node 101 as the source vertex. We show the steps below. When at 101, we mark this node as gray. Next, we visit its first undiscovered neighbor -- in this case, let us say 680. We mark 680 as gray again. Continuing the depth search, we again visit the first undiscovered neighbor of 680, which is 280. In this fashion, we reach the node 237. For 237, we have two neighbors (101 and 880), but both of them are discovered. So, we know that we are done with 237 and we mark it black. We also start backtracking. During backtracking, we go back to 880 and 680 and since neither of them have any neighbor with color as white, we mark both of them black. The node 101, however still has a neighbor as a white node, which is 280. Accordingly, we go from 101 to 280 and once we are done with 280, we come back to 101. It is easy to see this in the figure since the node 101 is the last node that we mark as black.
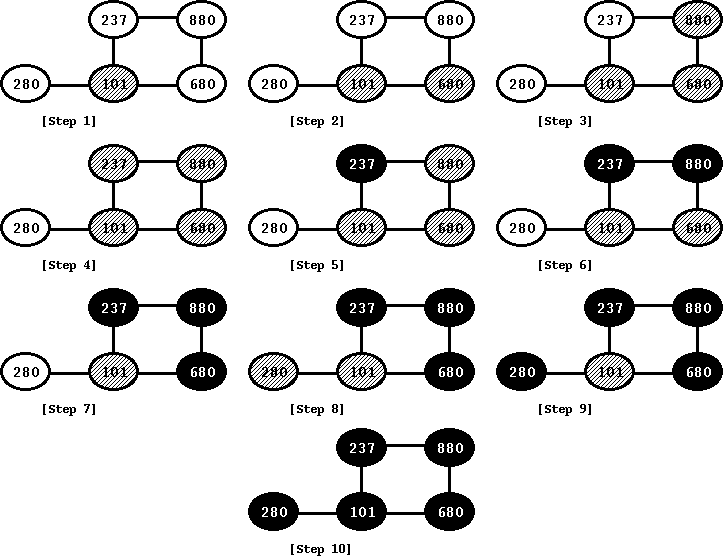
Figure: Depth-First Search
Depth-first search is different from the breadth-first search, where we start at a vertex and then cover all of its neighbors first, before moving on to the next set of neighboring vertices. Furthermore, we typically use an external data-structure (like queue) when using breadth-first search so that we can queue all the neighbors and process them one by one, before moving on to the next level of neighbors. Depth-first search can use recursion, where we do not have any external data-structure, but internally, the system is using the stack, where new functions calls pertaining to newer nodes get added at the top of the stack. Once we are done with the topmost node in the stack, we pop that context from the stack and go to the earlier one.
Implementation
Our depth-first-search takes help of Adjacency List data-structure. We cover this data-structure in our Data-Structure module. The reason why we reuse the existing implementation is that without doing that we would end up adding code for adjacency list in our implementation and that would make the code less readable. We recommend the reader to go through the adjacency-list module first.
The implementation of Adjacency List is provided in terms of both header file and an implementation file. For our depth-first-search implementation, we simply add the header file ("adjacency_list.h") and access the published APIs. In terms of APIs, we use the following APIs from adjacency list: adjlist_print() to print adjacency list, adjlist_add_vertex() to add a vertex to the adjacency list, adjlist_add_edge() to add an edge to the adjacency list, and adjlist_free() to free the adjacency list.
With that, let us provide the implementation of a depth-first search.
#include <stdio.h>
#include "adjacency_list.h"
void dfs_internal_run_recursively (vertex_node *graph_root, vertex_node *current_vnode) {
vertex_node *vnode = NULL;
edge_node *enode = NULL;
if (!current_vnode) {
return;
}
/* Start DFS */
printf("[%s] DFS: Working on Vertex: %d \n", __FUNCTION__, current_vnode->val);
for (enode = current_vnode->list_enode; enode != NULL; enode = enode->next_enode) {
vnode = (vertex_node *)enode->parent_vnode; /* Get the vertex node pointer. */
if (vnode->color == COLOR_WHITE) {
vnode->color = COLOR_GRAY;
dfs_internal_run_recursively(graph_root, vnode);
}
}
/* We are done with this node. */
current_vnode->color = COLOR_BLACK;
printf("[%s] Done with the node (%d)\n", __FUNCTION__, current_vnode->val);
adjlist_print(graph_root);
}
void dfs_run (vertex_node *graph_root) {
vertex_node *vnode = NULL;
if (!graph_root) {
return;
}
/* First, color all the vertices white. */
printf("\n[%s] Starting DFS. Color all Vertices as White\n", __FUNCTION__);
for (vnode = graph_root; vnode != NULL; vnode = vnode->next_vnode) {
vnode->color = COLOR_WHITE;
}
adjlist_print(graph_root);
/* Start by making the current node gray. */
graph_root->color = COLOR_GRAY;
dfs_internal_run_recursively(graph_root, graph_root);
printf("\n[%s] DFS Done\n", __FUNCTION__);
}
int main () {
vertex_node *graph_root = NULL; /* Root of the graph */
int vertices[] = {101, 237, 680, 280, 880};
int edges[][2] = {{101, 680}, {101, 237}, {880, 680}, {101, 280}, {237, 880}};
int len_vertices, len_edges, i;
/* Add the vertices. */
len_vertices = sizeof(vertices)/sizeof(vertices[0]);
for (i = 0; i < len_vertices; i++) {
adjlist_add_vertex(&graph_root, vertices[i], NULL);
}
/* Add the edges. */
len_edges = sizeof(edges)/sizeof(edges[0]);
for (i = 0; i < len_edges; i++) {
/* The third argument is the weight of the edge -- we keep it as 0 */
adjlist_add_edge(graph_root, edges[i][0], edges[i][1], 0);
}
/* Run DFS on this */
dfs_run(graph_root);
/* Done with the Adjacency List. Free it */
adjlist_free(&graph_root);
}
The above code contains functions that implement depth-first search. Let us begin with the main() function, where we build the adjacency list for the graph and triggers the depth-first search. For graph-building, we use input from two arrays: vertices and edges. Next, it calls djlist_add_vertex() to add vertices from the vertices array and adjlist_add_edge() to add edges from the edges array. Once that is done, it calls dfs_fun() with the the root of the graph (which is also a vertex) as the source vertex. The dfs_fun() colors all the vertices as white and then calls dfs_internal_run_recursively() starting with the graph root. Once dfs_run() returns, it calls adjlist_free() API to free the adjacency list.
The dfs_internal_run_recursively() is at the heart of the depth-first search. For depth-first search, we use this function once for each vertex node. When visiting a vertex node, we walk through all of its neighboring vertices and if we find any vertex that has not been visited, then we recursively call dfs_internal_run_recursively() for that neighbor vertex. Since recursion traverses back in the stack, once we are done with the neighbor vertex, the recursion would automatically go back to its parent vertex and so on till we reach the root of the graph (or the vertex, where we started). If using recursion can get expensive (some of the systems have a default limit on the number of recursion calls), then we can try to take the help of an external stack data-structure.
Let us consider the time complexity of the depth-first search. We start at a vertex and then traverse its first vertex, and then traverse the first vertex of this vertex and so on. However, if we find a vertex that has already been visited or is being visited, then we skip that. Thus, the total number of times we process the vertex nodes is O(V). In terms of edges, whenever we visit a vertex for the first-time, we walk through all of its edges. Since we visit each edge node twice, the total number of times we process the edges is O(E). Thus, the total running time complexity of depth-first search is O(E + V). Thus, it is linear with respect to edges and vertices. Please note that even with with breadth-first search, the time complexity is also linear in terms of edges and vertices.
user@codingbison $ gcc dfs.c adjacency_list.c -o dfs
user@codingbison $ ./dfs
[dfs_run] Starting DFS. Color all Vertices as White
[adjlist_print] Print the Adjacency List
Vertex [101][Color: 1]: -- Edge [680 (0)] -- Edge [237 (0)] -- Edge [280 (0)]
Vertex [237][Color: 1]: -- Edge [101 (0)] -- Edge [880 (0)]
Vertex [680][Color: 1]: -- Edge [101 (0)] -- Edge [880 (0)]
Vertex [280][Color: 1]: -- Edge [101 (0)]
Vertex [880][Color: 1]: -- Edge [680 (0)] -- Edge [237 (0)]
[dfs_internal_run_recursively] DFS: Working on Vertex: 101
[dfs_internal_run_recursively] DFS: Working on Vertex: 680
[dfs_internal_run_recursively] DFS: Working on Vertex: 880
[dfs_internal_run_recursively] DFS: Working on Vertex: 237
[dfs_internal_run_recursively] Done with the node (237)
[adjlist_print] Print the Adjacency List
Vertex [101][Color: 2]: -- Edge [680 (0)] -- Edge [237 (0)] -- Edge [280 (0)]
Vertex [237][Color: 3]: -- Edge [101 (0)] -- Edge [880 (0)]
Vertex [680][Color: 2]: -- Edge [101 (0)] -- Edge [880 (0)]
Vertex [280][Color: 1]: -- Edge [101 (0)]
Vertex [880][Color: 2]: -- Edge [680 (0)] -- Edge [237 (0)]
[dfs_internal_run_recursively] Done with the node (880)
[adjlist_print] Print the Adjacency List
Vertex [101][Color: 2]: -- Edge [680 (0)] -- Edge [237 (0)] -- Edge [280 (0)]
Vertex [237][Color: 3]: -- Edge [101 (0)] -- Edge [880 (0)]
Vertex [680][Color: 2]: -- Edge [101 (0)] -- Edge [880 (0)]
Vertex [280][Color: 1]: -- Edge [101 (0)]
Vertex [880][Color: 3]: -- Edge [680 (0)] -- Edge [237 (0)]
[dfs_internal_run_recursively] Done with the node (680)
[adjlist_print] Print the Adjacency List
Vertex [101][Color: 2]: -- Edge [680 (0)] -- Edge [237 (0)] -- Edge [280 (0)]
Vertex [237][Color: 3]: -- Edge [101 (0)] -- Edge [880 (0)]
Vertex [680][Color: 3]: -- Edge [101 (0)] -- Edge [880 (0)]
Vertex [280][Color: 1]: -- Edge [101 (0)]
Vertex [880][Color: 3]: -- Edge [680 (0)] -- Edge [237 (0)]
[dfs_internal_run_recursively] DFS: Working on Vertex: 280
[dfs_internal_run_recursively] Done with the node (280)
[adjlist_print] Print the Adjacency List
Vertex [101][Color: 2]: -- Edge [680 (0)] -- Edge [237 (0)] -- Edge [280 (0)]
Vertex [237][Color: 3]: -- Edge [101 (0)] -- Edge [880 (0)]
Vertex [680][Color: 3]: -- Edge [101 (0)] -- Edge [880 (0)]
Vertex [280][Color: 3]: -- Edge [101 (0)]
Vertex [880][Color: 3]: -- Edge [680 (0)] -- Edge [237 (0)]
[dfs_internal_run_recursively] Done with the node (101)
[adjlist_print] Print the Adjacency List
Vertex [101][Color: 3]: -- Edge [680 (0)] -- Edge [237 (0)] -- Edge [280 (0)]
Vertex [237][Color: 3]: -- Edge [101 (0)] -- Edge [880 (0)]
Vertex [680][Color: 3]: -- Edge [101 (0)] -- Edge [880 (0)]
Vertex [280][Color: 3]: -- Edge [101 (0)]
Vertex [880][Color: 3]: -- Edge [680 (0)] -- Edge [237 (0)]
[dfs_run] DFS Done
The output pretty much shows the steps that we have outlined in earlier figure. We start with node 101 and then travel to nodes 680, 880, and 237. Once we reach 237, we have no more new neighbors and so we backtrack to 101 again. The 101 still has a new neighbor (280) and only after we traverse that node, we come back to 101 again. At the end, all nodes are traversed and accordingly, mark them black.