Dijkstra's Algorithm
We can use Dijkstra's Algorithm to find the shortest path from a given node (let us call it, the single source) to all the other nodes in a weighted graph. Thus, in the following graph with weight of an edge showing the cost of going from one vertex to another, if we need to find the shortest path from a source-node (let us say 101) to all other nodes, then we can the Dijkstra's algorithm. The result of this algorithm would tell that we can reach node 680 with a cost of 12, we can reach node 880 with a cost of 14, and so on.
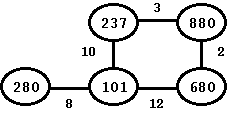
Figure: An undirected Graph with Weights
Dijkstra's algorithm shares certain similarity with Prim's algorithm, let us compare them briefly. Prim's algorithm builds a minimum spanning tree -- a tree that spans all the (connected) nodes in the graph and the sum of weights of all edges is the minimum. Dijkstra's algorithm does no such thing. Instead, it calculates the shortest path (the path with least total weight) from a given root node to all the other nodes in the (connected) graphs. In terms of methodology, they both start with a source vertex (node) and proceed from there. Another similarity is that both of these algorithms use breadth-first search approach and (typically) use a heap to get the next vertex node.
Dijkstra's algorithm works with both directed and undirected graph. In terms of limitations of this algorithm, Dijkstra's algorithm assumes that all edges are non-negative. In our example, we use an undirected graph.
So, how does it work?
Dijkstra's algorithm works by growing a tree such that its holds the property that all vertices from a given vertex (the source) have the shortest path from the source vertex. At each stage, the algorithm selects a new edge such that the tree grows but it still maintains the property. When doing so, it adds a new vertex node from that edge. This is done repetitively till all the vertices are added to the tree. Since at each stage, all edges of the newly added vertex are added, this confirms that Dijkstra's algorithm uses breadth-first search approach. Accordingly, at any point, it works by expanding the breadth of the current shortest-path tree. One minor note. You might think that even though Dijkstra's algorithm uses a breadth-first search approach, it does not rely on a queue. Instead, it uses a heap since not only does it need to consider all immediate edges, it also needs to know the edge with the least weight.
Let us use the above figure to go through various steps in the Dijkstra's algorithm. Following that, we provide our implementation. To start the steps, the application would need to pass the source node with respect to which, we would like to run the Dijkstra's algorithm. For our case, we start with the node that has a value of 101 in the above figure. As we keep adding nodes to the tree, we keep coloring those nodes as black. Further, as we build the tree, we would mark the nodes as blue. Thus, at any time, the Dijkstra's shortest tree is represented by the black edges. Since once we are done with a node, we are done with immediately and hence, there is no real need to mark the node as gray -- we go straight from white to black.
Once we have the source-node, we can can get the ball rolling. The very first step is to add all the edges belonging to the source node to the heap. In this case, with source node as 101, the heap would contain all the three edges: 101-280, 101-237, and 101-680. The heap is a min-heap and the extraction happens based on the weight of these edges. Next, we mark the source node as black -- we are done with it. We provide the graph below showing this first step. The figure also shows the heap and the distance array. The heap contains all the edges that are in consideration. The distance array shows the distance for each node from the source-node and the parent node for each node.
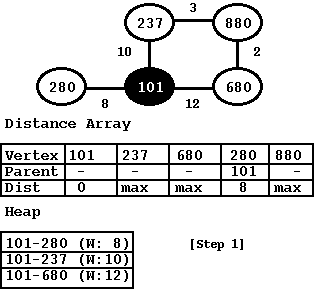
Figure: Step 1: Select source node (101) and adds its edges to Heap
The next set of steps can be added in a while loop. We extract the minimum edge from the heap, add the vertices that are not black and then update the distance array to compute the distance of this vertex to the source node. To do that, we walk all the vertex nodes that are adjacent to the new vertex and for each adjacent vertex node, we recompute the distance of the new vertex to the source node. We select the distance that is the least. Please note that, when walk the list of adjacent vertex nodes, we ignore those vertices that are not yet added to the tree. In this step, then we extract the next node form the heap (101-280). We mark the node 280 since we are done with it. Also, we do not have to add any new edges to heap since 280 has no new edges.
Accordingly, the next step is similar to the earlier step. We extract the least edge (101-237) from the heap. The vertex 237 has a new edge, 237-680 and we add it to the heap. Since we are done with 237, we mark it black and recompute the distances in the distance vector.
From the above state, next we extract edge 237-680. For 680, we compute its distance to the source node. Now it has two paths. First path is 101 to 237 to 680, which has a total weight of 15 (10+5). The second path is 101 to 680 directly, which has a total weight of 12. So, we would prefer this and mark 101 as its parent. We mark 680 as black since we are done with it. At this point, the heap has no element and that terminates the Dijkstra's algorithm.
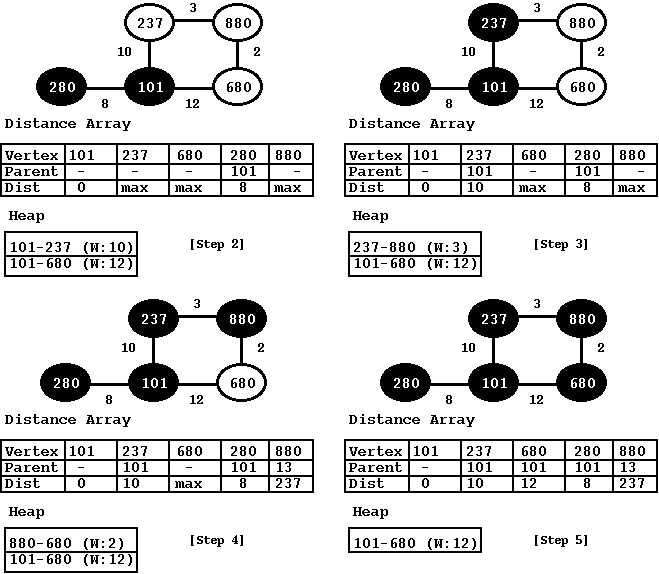
Figure: Rest Steps: Add vertices one-by-one to the Dijkstra tree
Implementation
In terms of implementation, we would need a few things. First, we need a way to represent the graph -- this can be either an adjacency list or an adjacency matrix. In our implementation, we use an adjacency matrix. Second, to identify all the vertex nodes that are already added in the tree, the implementation must be able to mark each node with a new color. When we start, we mark all the nodes with white color (akin to the above figure, if you would like!) and once we add a vertex to Dijkstra's tree, we mark it black. Third, we need a min-heap or an equivalent data-structure. Dijkstra algorithm relies on a heap to keep a set of edges so that it can extract the edge with the least weight. Fourth, we need an array that stores the distance from the source-node (let us say, 101) to all other nodes in the graph and the immediate parent of each node. For the sake of run-time efficiency, we use a member of the vertex node to point each vertex node to its index in the array. Not doing so would mean we would end up searching the array multiple times and that can be inefficient.
Accordingly, we take help of our existing implementation for Adjacency List and Heap. We have added both of these modules in our Data-Structure module. The main reason why we reuse these two existing implementations is that without doing that we would end up implementing both adjacency list and heap in our implementation. And that would bloat things! Our implementation of these data-structures Heap are provided in terms of both header file and an implementation file. We recommend the reader to go through these two implementations first.
For our Dijkstra's implementation, we simply add the header files ("adjacency_list.h" and "heap.h") of the above implementation so that we can access their APIs. Speaking of APIs, we use the following APIs from adjacency list: adjlist_add_vertex() to add a vertex to the adjacency list, adjlist_add_edge() to add an edge to the adjacency list, adjlist_free() to free the adjacency list, and adjlist_print() to print adjacency list. For heap, we use the following APIs: heap_init() to initialize the heap, heap_add() to add edges to the heap, and heap_extract() to pop the edge with the smallest weight; we pass dijkstra_heap_compare() to the heap_init() API so that we can use dijkstra_heap_compare() to compare two of the Dijkstra's edge nodes.
This implementation (provided below) also uses a new data-structure, dijkstra_edge_nodes that holds two vertex nodes and its weight. The implementation also has a handful of global variables. First one is the arr_distance that is a 2-dimensional array that holds distance and the parent-node for each vertex node. The next one is the len_arr_distance, which holds the current length of the nodes in the array. In this array, the first row is the vertex nodes that are present in the graph, the second row is the parent node corresponding to each vertex and the last row holds the distance of that node from the source vertex. The next global variable is the graph_root, which is the root of the graph.
#include <stdio.h>
#include <stdlib.h>
#include <math.h>
#include <limits.h>
#include "adjacency_list.h"
#include "heap.h"
#define MAX_ELEMENTS 32
/* Represents an edge (has both sides, represented as vnode) and the edge weight. */
typedef struct dijkstra_edge_nodes_ {
vertex_node *vnodeA;
vertex_node *vnodeB;
int weight; /* Weight of the Edge */
} dijkstra_edge_nodes;
/* The global variables */
int arr_distance[MAX_ELEMENTS][3]; /* Double-array that holds all the distances */
int len_arr_distance; /* Max Length of the above array */
vertex_node *graph_root = NULL; /* Root of the graph */
int dijkstra_heap_compare (const void *val1, const void *val2) {
dijkstra_edge_nodes *node1 = (dijkstra_edge_nodes *)val1;
dijkstra_edge_nodes *node2 = (dijkstra_edge_nodes *)val2;
if (node1->weight < node2->weight) {
return -1;
} else if (node1->weight > node2->weight) {
return 1;
} else {
return 0;
}
}
void dijkstra_heap_print (heap_t *heap) {
dijkstra_edge_nodes *node, *parent;
int counter = 0;
printf("Printing the Heap: \n");
if ((heap == NULL) || (heap->heap_current_size == 0)) {
printf("Heap is Empty\n");
return;
}
for (counter = 0; counter < heap->heap_current_size; counter++) {
node = (dijkstra_edge_nodes *)heap->heap_array[counter];
parent = (dijkstra_edge_nodes *)(heap->heap_array[(int) floor((double)(counter-1)/2)]);
if (counter == 0) {
printf("\t[i: %d] %2d-%2d (Weight: %2d Parent: NULL)\n",
counter, node->vnodeA->val, node->vnodeB->val, node->weight);
} else {
printf("\t[i: %d] %2d-%2d (Weight: %2d Parent: %d-%d)\n",
counter, node->vnodeA->val, node->vnodeB->val, node->weight,
parent->vnodeA->val, parent->vnodeB->val);
}
}
printf("\n");
}
void dijkstra_print_distance_array (void) {
int i;
printf("Distance Array: ");
for (i = 0; i < len_arr_distance; i++) {
printf("%d (p: %d, d: %d) ",
arr_distance[i][0], arr_distance[i][1], arr_distance[i][2]);
if (((i+1) % 3) == 0) { /* Add a new line every 3 nodes */
printf("\n\t\t");
}
}
printf("\n");
}
void dijkstra_add_my_edges_to_heap (vertex_node *vnode, heap_t *heap) {
dijkstra_edge_nodes *both_enodes;
edge_node *enode;
for (enode = vnode->list_enode; enode != NULL; enode = enode->next_enode) {
if (((vertex_node *)enode->parent_vnode)->color == COLOR_BLACK) {
continue; /* Already added. Skip it. */
}
both_enodes = (dijkstra_edge_nodes *)malloc(sizeof(dijkstra_edge_nodes));
if (!both_enodes) {
return;
}
both_enodes->vnodeA = vnode;
both_enodes->vnodeB = enode->parent_vnode;
both_enodes->weight = enode->weight;
heap_add(heap, (void *)both_enodes);
}
}
void dijkstra_add_edge_to_distance_array (dijkstra_edge_nodes *both_enode) {
vertex_node *vnode = NULL;
edge_node *enode;
int new_vnode_index, vnode_index, new_dist, old_dist;
printf("Selecting Edge (%d-%d) with weight: %d\n",
both_enode->vnodeA->val, both_enode->vnodeB->val, both_enode->weight);
vnode = (both_enode->vnodeA->color == COLOR_WHITE) ?
both_enode->vnodeA : both_enode->vnodeB;
new_vnode_index = vnode->misc_index;
printf("Adding Vertex node %d (Distance Array index: %d) \n",
vnode->val, new_vnode_index);
/* Walk through each attached edge node and then reevaluate the distance */
for (enode = vnode->list_enode; enode != NULL; enode = enode->next_enode) {
if (((vertex_node *)enode->parent_vnode)->color == COLOR_WHITE) {
/* Don't bother with vertices that are not yet added to the tree */
continue;
}
vnode_index = ((vertex_node *)enode->parent_vnode)->misc_index;
new_dist = arr_distance[vnode_index][2] + enode->weight;
old_dist = arr_distance[new_vnode_index][2];
if (new_dist < old_dist) {
printf("New distance (%d) is less than the earlier (%d). Update\n",
new_dist, old_dist);
arr_distance[new_vnode_index][1] = ((vertex_node *)enode->parent_vnode)->val;
arr_distance[new_vnode_index][2] = new_dist;
} else {
printf("New distance (%d) is more than the earlier (%d). Skip\n",
new_dist, arr_distance[new_vnode_index][2]);
}
}
dijkstra_print_distance_array();
}
void dijkstra_run (heap_t *heap, vertex_node *source_vertex) {
dijkstra_edge_nodes *both_enode;
vertex_node *vnode, *new_vnode;
int err, i;
/* First things first. Let us do some initialization. */
for (i = 0; i < len_arr_distance; i++) {
arr_distance[i][0] = 0;
arr_distance[i][1] = 0;
arr_distance[i][2] = INT_MAX;
}
for (vnode = graph_root, i = 0; vnode != NULL; vnode= vnode->next_vnode, i++) {
vnode->misc_index = i;
vnode->color = COLOR_WHITE;
arr_distance[i][0] = vnode->val;
}
/* All set. Start the while loop at the source vertex */
dijkstra_add_my_edges_to_heap(source_vertex, heap);
source_vertex->color = COLOR_BLACK;
arr_distance[source_vertex->misc_index][2] = 0;
while (heap->heap_current_size) {
/* Print the Heap */
adjlist_print(graph_root);
dijkstra_heap_print(heap);
/* Extract the Minimum */
both_enode = (dijkstra_edge_nodes *)heap_extract(heap, &err);
if (!both_enode || !both_enode->vnodeA || !both_enode->vnodeB) {
if (both_enode) {
free(both_enode);
break;
}
}
/* Find the unmarked vertex. Add its edges to Heap. */
if ((both_enode->vnodeA) && (both_enode->vnodeA->color == COLOR_WHITE)) {
new_vnode = both_enode->vnodeA;
} else {
if ((both_enode->vnodeB) && (both_enode->vnodeB->color == COLOR_WHITE)) {
new_vnode = both_enode->vnodeB;
}
}
if (new_vnode) {
dijkstra_add_edge_to_distance_array(both_enode);
new_vnode->color = COLOR_BLACK; /* Done with this node -- mark it black */
dijkstra_add_my_edges_to_heap(new_vnode, heap);
}
free(both_enode);
new_vnode = NULL;
}
}
int main () {
heap_t heap;
int vertices[] = {101, 237, 680, 280, 880};
int edges[][3] = {{101, 680, 12}, {101, 237, 10}, {880, 680, 2},
{101, 280, 8}, {237, 880, 3}};
vertex_node *source_vertex = NULL, *vnode = NULL;
int len_vertices, len_edges, i;
/* Init the heap */
heap_init(&heap, dijkstra_heap_compare);
/* Add vertices. */
len_vertices = sizeof(vertices)/sizeof(vertices[0]);
len_arr_distance = len_vertices;
for (i = 0; i < len_vertices; i++) {
adjlist_add_vertex(&graph_root, vertices[i], NULL);
}
/* Add the edges. */
len_edges = sizeof(edges)/sizeof(edges[0]);
for (i = 0; i < len_edges; i++) {
adjlist_add_edge(graph_root, edges[i][0], edges[i][1], edges[i][2]);
}
/* Run the Dijkstra's Algorithm */
dijkstra_run(&heap, graph_root);
dijkstra_heap_print(&heap);
/* Done with the Adjacency List. Free it */
adjlist_free(&graph_root);
}
For the sake of simplicity, the main() function uses the same graph as before -- a graph with 5 vertices and 5 edges. You are more than welcome to try the above code with higher number of vertices and edges! Further, for the sake of simplicity, some of the functions do not have a NULL-check for arguments passed to them. If you are going to use this code to write a production-style software, please do add NULL-check, where ever they are applicable.
The main() function uses the adjlist_add_vertex() and adjlist_add_edge() APIs from the "adjacency_list.h" to add vertex and edges to the graph_root. Once the graph is build, the main() function runs dijkstra_run() with the graph_root as the source node.
The dijkstra_run() runs a while loop, where at each step a vertex node is added to the tree. When a vertex is added, all of its edge are added to the heap, if they are not already present. This function uses heap_add() to add edges to the heap and heap_extract() to extract the edge with the minimum weight. For adding new edges of the selected vertex node, it relies upon the dijkstra_add_my_edges_to_heap() function.
When dijkstra_run() adds a new node to the tree, it calls dijkstra_add_edge_to_distance_array() to update the distance array. This function is pretty much at the heart of Dijkstra's algorithm. This function takes the edge and then finds the vertex node that has not been added yet (by checking if the color is COLOR_WHITE). When it finds it, it walks through all the edges of that node. When doing the walk, it calculates its distance from the source-node for each of the adjacent nodes. If it finds that the distance is smaller than the earlier one, then it replaces the distances and also updates its parent to point to the new edge. For example, in Step 4 in the earlier picture, when we are adding the vertex 680, it compares its distance from source via both of its adjacent vertices (237 and 101). It finds that the distance via 237 is 15 (10+5) and the distance via 101 is only 12 and so it chooses 12 and updates it parent to 101.
In terms of output, the above implementation offers couple of routines. The dijkstra_heap_print() prints the heap and shows edges present in the heap with their weights. The dijkstra_print_distance_array() prints the distance array; for each vertex node, it prints its parent and its distance from the source node. And of course, it also uses adjlist_print() to print all elements in the graph -- this print routine is offered by our adjacency list implementation.
Next, we compile the above program. One minor detail. When compiling "adjacency_list.c", we keep the value of the global debug variable (adjlist_print_debug) in the adjacency_list.c file to be false -- this saves a dozen of lines of debugs and thus, makes the output a little simpler.
user@codingbison $ gcc dijkstra.c adjacency_list.c heap.c -lm -o dijkstra
user@codingbison $ ./dijkstra
[adjlist_print] Print the Adjacency List
Vertex [101][Color: 3]: -- Edge [680 (12)] -- Edge [280 (8)] -- Edge [237 (10)]
Vertex [237][Color: 1]: -- Edge [101 (10)] -- Edge [680 (5)]
Vertex [680][Color: 1]: -- Edge [101 (12)] -- Edge [237 (5)]
Vertex [280][Color: 1]: -- Edge [101 (8)]
Printing the Heap:
[i: 0] 101-280 (Weight: 8 Parent: NULL)
[i: 1] 101-237 (Weight: 10 Parent: 101-280)
[i: 2] 101-680 (Weight: 12 Parent: 101-280)
Selecting Edge (101-280) with weight: 8
Distance Array:
101 (p: 0, d: 0) 237 (p: 0, d: 2147483647) 680 (p: 0, d: 2147483647) 280 (p: 0, d: 2147483647)
Adding Vertex node 280 (Distance Array index: 3)
New distance (8) is less than the earlier (2147483647). Update
Distance Array:
101 (p: 0, d: 0) 237 (p: 0, d: 2147483647) 680 (p: 0, d: 2147483647) 280 (p: 101, d: 8)
[adjlist_print] Print the Adjacency List
Vertex [101][Color: 3]: -- Edge [680 (12)] -- Edge [280 (8)] -- Edge [237 (10)]
Vertex [237][Color: 1]: -- Edge [101 (10)] -- Edge [680 (5)]
Vertex [680][Color: 1]: -- Edge [101 (12)] -- Edge [237 (5)]
Vertex [280][Color: 3]: -- Edge [101 (8)]
Printing the Heap:
[i: 0] 101-237 (Weight: 10 Parent: NULL)
[i: 1] 101-680 (Weight: 12 Parent: 101-237)
Selecting Edge (101-237) with weight: 10
Distance Array:
101 (p: 0, d: 0) 237 (p: 0, d: 2147483647) 680 (p: 0, d: 2147483647) 280 (p: 101, d: 8)
Adding Vertex node 237 (Distance Array index: 1)
New distance (10) is less than the earlier (2147483647). Update
Distance Array:
101 (p: 0, d: 0) 237 (p: 101, d: 10) 680 (p: 0, d: 2147483647) 280 (p: 101, d: 8)
[adjlist_print] Print the Adjacency List
Vertex [101][Color: 3]: -- Edge [680 (12)] -- Edge [280 (8)] -- Edge [237 (10)]
Vertex [237][Color: 3]: -- Edge [101 (10)] -- Edge [680 (5)]
Vertex [680][Color: 1]: -- Edge [101 (12)] -- Edge [237 (5)]
Vertex [280][Color: 3]: -- Edge [101 (8)]
Printing the Heap:
[i: 0] 237-680 (Weight: 5 Parent: NULL)
[i: 1] 101-680 (Weight: 12 Parent: 237-680)
Selecting Edge (237-680) with weight: 5
Distance Array:
101 (p: 0, d: 0) 237 (p: 101, d: 10) 680 (p: 0, d: 2147483647) 280 (p: 101, d: 8)
Adding Vertex node 680 (Distance Array index: 2)
New distance (12) is less than the earlier (2147483647). Update
New distance (15) is more than the earlier (12). Skip
Distance Array:
101 (p: 0, d: 0) 237 (p: 101, d: 10) 680 (p: 101, d: 12) 280 (p: 101, d: 8)
[adjlist_print] Print the Adjacency List
Vertex [101][Color: 3]: -- Edge [680 (12)] -- Edge [280 (8)] -- Edge [237 (10)]
Vertex [237][Color: 3]: -- Edge [101 (10)] -- Edge [680 (5)]
Vertex [680][Color: 3]: -- Edge [101 (12)] -- Edge [237 (5)]
Vertex [280][Color: 3]: -- Edge [101 (8)]
Printing the Heap:
[i: 0] 101-680 (Weight: 12 Parent: NULL)
[adjlist_print] Print the Adjacency List
Vertex [101][Color: 3]: -- Edge [680 (12)] -- Edge [280 (8)] -- Edge [237 (10)]
Vertex [237][Color: 3]: -- Edge [101 (10)] -- Edge [680 (5)]
Vertex [680][Color: 3]: -- Edge [101 (12)] -- Edge [237 (5)]
Vertex [280][Color: 3]: -- Edge [101 (8)]
Distance Array:
101 (p: 0, d: 0) 237 (p: 101, d: 10) 680 (p: 101, d: 12) 280 (p: 101, d: 8)
The above output is similar to what we had discussed before in the figures. However, there are couple of things worth noting. First, as we build the Dijkstra's tree, the color of nodes go from white (value 1) to black (value 3). Second, for the source-node, both the parent and the distance row remain its initial values (which is zero).
To make the above implementation more generic, we have two recommendations. First would be that we should make these variables have a more tighter scope -- we do not do that here since we want to keep the implementation simple. Second, we keep the maximum length of the array to be MAX_ELEMENTS -- for a generic implementation, we should consider allocating the array dynamically.